The plane

Least Square Method (LSM) task is the subject of Analytic Geometry and is realized in 3D Euclidean vector space with Cartesian coordinate system and is formulated to find an orthogonal projection in 2D subspace of any vector. In general, LSM itself is a significant part of computation mathematics from the solution of differential equations (boundary value problems) to statistics and vary  in realizations implied by the type of vector spaces.

To solve this task in IMIMS environment students should know the following notions and be able to apply them by performing computations with Octave software: Euclidean space, Cartesian coordinate system, vectors, subspaces and their relations to (hiper)planes, basis of space and subspace, scalar product of vectors, orthogonality, solution of linear system of equations.

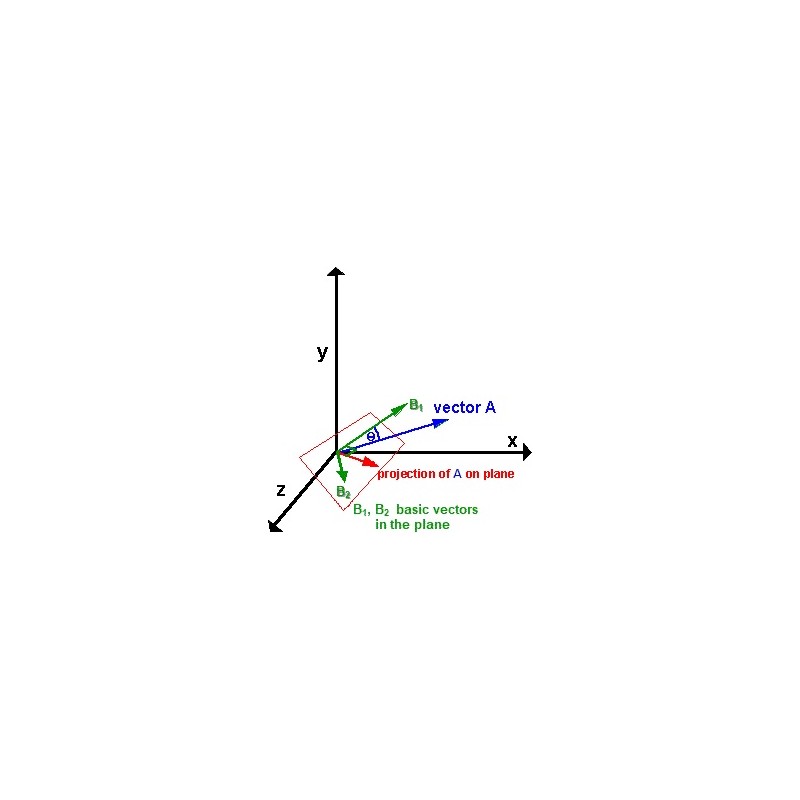
The task consist of projection vector pr computation in 2D subspace of any vector v=[v_x,v_y,v_z] in 3D space, i.e. projection in the plane crossing the origin of coordinate system. Analytically this plane is represented by the equation ax+by+cz+d=0, where coefficient d=0 and corresponds to the 4-dimensional vector pln=[a,b,c,0], representing this plane. The basic vectors in the plane are denoted by b1=[b1_x, b1_y, b1_z] and b2=[b2_x, b2_y, b2_z] respectively. Then projection vector pr of vector v must be expressed by a linear combination of basic vectors b1 and b2 and hence will have two coordinates, i.e. pr=[pr_x, pr_y].

To solve the task student must step by step recursively enter 5 input data. We present here the following test example.

1-st Step. Student chooses plane vector pln=[1, -1, 1, 0] and enters it in the first input field:

[1, -1, 1, 0]        then clicks the button Check Result.

Server returns a picture of coordinate system and plane.

2-nd Step. Student using Octave editor in IMIMS window below (or MatLab package) computes the basis, consisting of two vectors b1 and b2 in the plane he/she have been chosen. He/she enters the coordinates of these vectors in two fields below. In our test example it will be:

[5, 5, 0]

[5, 0, -5]            then clicks the button Check Result.

If basis vectors are computed correctly, server returns a picture of coordinate system, plane and two basic vectors depicted.

3-rd Step. Student chooses 3D vector v to compute its projection on the plane:

[3, 4, 5] then clicks the button Check Result.

Server returns a picture of coordinate system, plane, two basic vectors and vector v depicted.

4-rd Step. Student using Octave editor in IMIMS window below computes projection vector pr expressed as a linear combination of two basic vectors b1 and b2. It is required to enter the components of obtained vector as a fraction. These fractions are entered in the last input field:

[16/15, -11/15] then Check Result button is clicked.

If projection vector pr is computed correctly, server returns a picture of coordinate system, plane, two basic vectors, vector v and vector pr depicted.